Correlating Activation Energy with Relevant Orbital Energy
QM Magic Class | Chapter 44
Ying Lu, Zhong Zheng, Yongsheng Chen, John S. Wai
< Magical Power of Quantum Mechanics
In Chapter 25 “Assessing Reactivity with LUMO and HOMO Energy Gap“, we discussed nucleophilicity and electrophilicity of substrate/reagent can be evaluated by their HOMO and LUMO energies, respectively, and the correlation between reactivity and LUMO and HOMO Energy Gap. In this chapter, we will analyze further such correlations between orbital energies and activation energies in nucleophilic aromatic substitution reactions.
SnAr Reaction of Substituted 2-Fluoropyridines
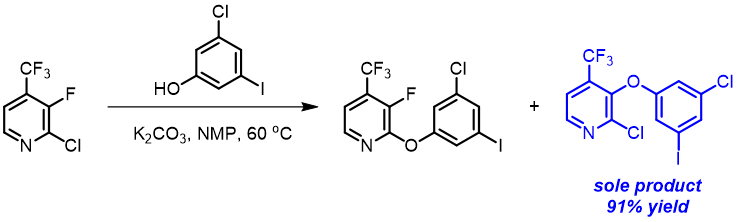
2-Fluoropyridine undergoes SnAr reaction with sodium ethoxide in EtOH about 250 times faster than 2-chloropyridine [1]. The activating effects of various substituents on the displacement of 2-fluoropyridine will be of great interest to medicinal and organic chemists. Schlosser et al [2] reported that by mixing equal amount of 2-fluoropyridine and its substituted analogs and reacting the mixture with sub-stoichiometric amount of sodium ethoxide in ethanol, monitoring the disappearance of the substrates and appearance of products, the relative reaction rate of each reaction substrate relative to 2-fluoropyridine and the relative activation free energy ΔΔG could be calculated (Table 1).

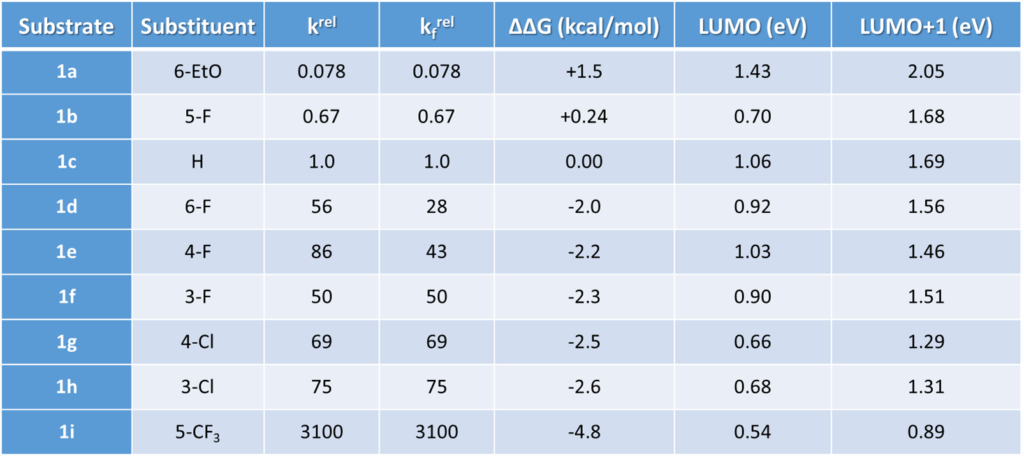
LUMO and LUMO+1 energies of the fluoropyridine substrates, calculated with DFT ωB97X-D/6-31G*, are tabulated. Linear regression analysis on the LUMO orbital energy level versus the relative activation energy obtained from the experiment plot shows poor linear correlation, with a coefficient of determination (R2) of 0.5379 (Figure 1).
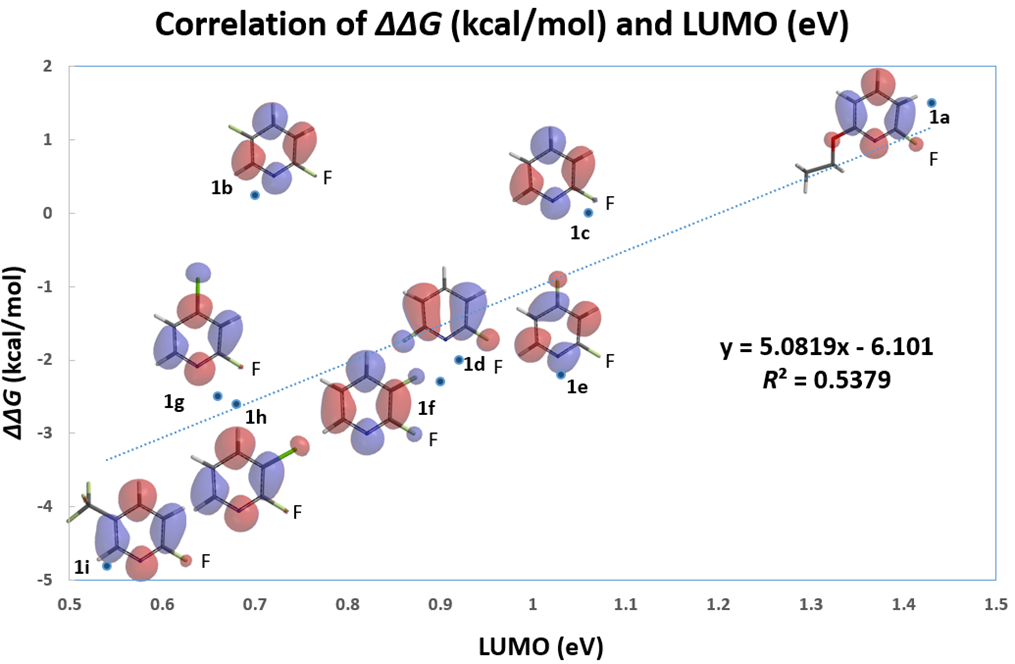
We noticed little to none LUMO lobe centered on the C-F carbon with these 2-fluoropyridines, indicating that the associated LUMO energy data may not be relevant for correlation analysis of this set of fluoride displacement reactions. Galabov et al. also reported a similar weak correlation in electrophilic aromatic substitution reactions [3].
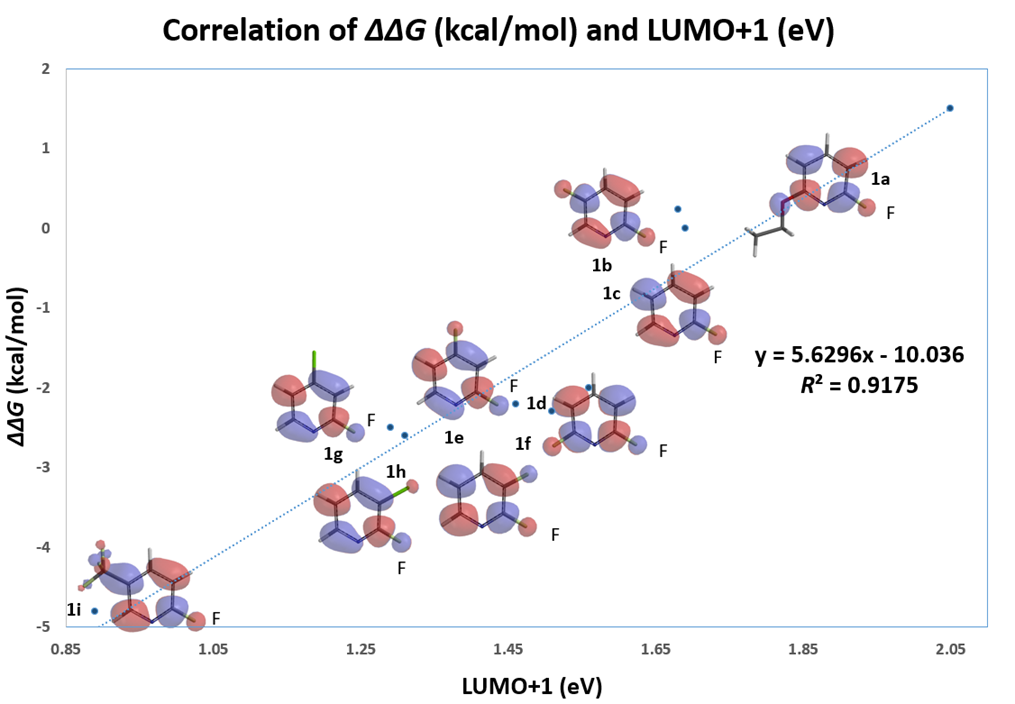
On the other hand, with LUMO+1, there are significant lobes centered on C-F carbon of this set of 2-fluoropyridines (Figure 2). Linear correlation of their LUMO+1 energies and the activation energies is excellent, with a coefficient of determination (R2) of 0.9175, significant improvement as compared to the use of LUMO. This shows that it is necessary to select only the relevant frontier orbitals, and the associated orbital energy values, for reactivity analyses. These are crucial prerequisites for successful Quantum Mechanics-Machine Learning of chemical reactivity and regioselectivity.
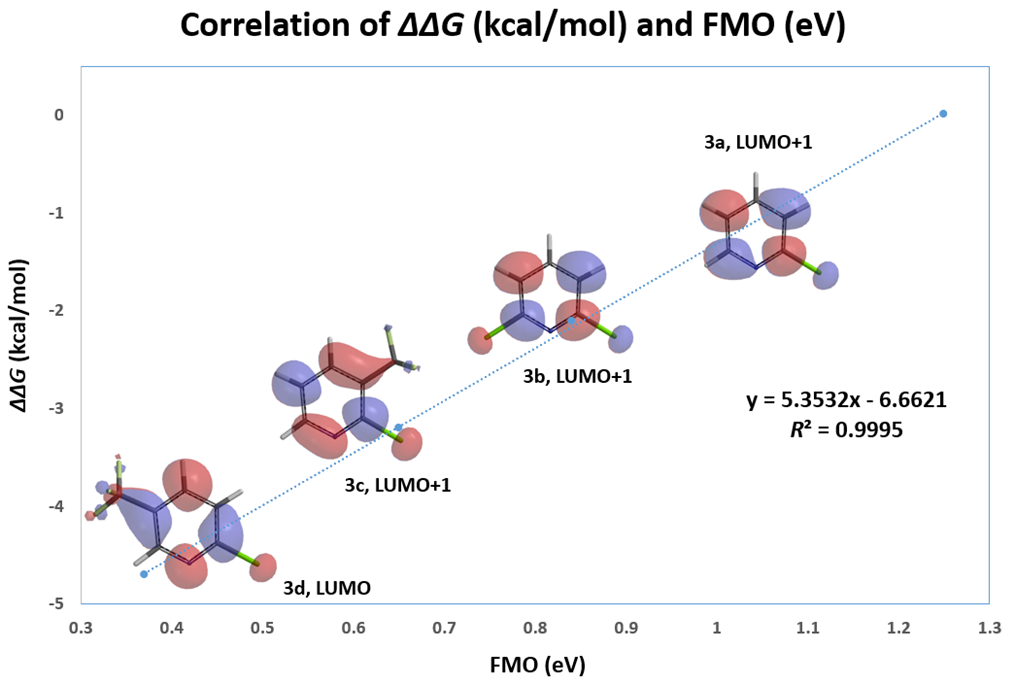
This lesson could be further exemplified with the SnAr reaction of various substituted 2-chloropyridines. Excellent linear correlation (R2 of 0.9995) of reactivity with relevant LUMO or LUMO+1 orbital energy, chosen with an orbital lobe centered on the C-Cl carbon (Figure 3, Table 2). Relevant orbitals for correlation of a set of electrophiles with reactivity could be a mix of LUMO and LUMO+n. We need to choose the appropriate ones first.

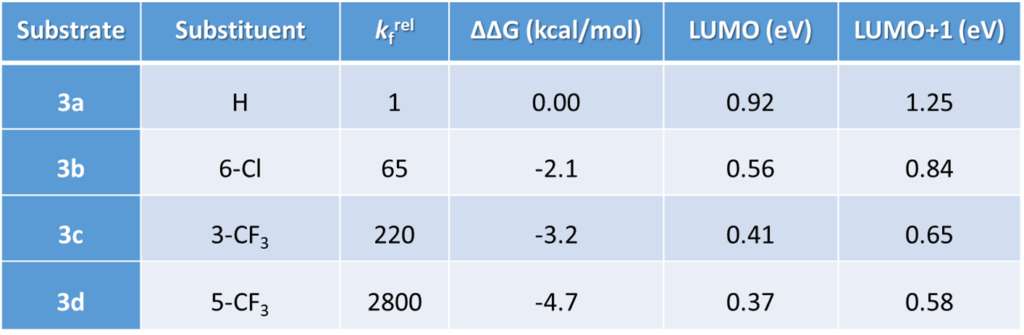
The resultant linear regression equations obtained from above correlations could be used to infer reactivity of other 2-chloro/fluoropyridine analogs (Figures 2 & 3). For example, with 2,6-dichloro-3-trifluoromethylpyridine (Figure 4), LUMO has a lobe centered on C6-Cl carbon, while LUMO+1 has a lobe centered on C2-Cl carbon. Substituting the energy value of LUMO (0.11 eV) and LUMO+1 (0.26 eV) into the linear regression equation in Figure 3 provided ΔΔG of -6.07 kcal/mol for reaction at C-6 vs -5.27 kcal/mol for reaction at C2, respectively (the negative sign indicates their ΔG are smaller than that for 2-chloropyridine). As such, chloride displacement at C6 will be much faster than at C2, consistent with experimental numbers of ΔΔG -6.5 kcal/mol and -5.4 kcal/mol, respectively, reported [2]. Steric hindrance effect of trifluoromethyl group is anticipated to slow down nucleophilic attack at C2 further, resulting in C6 displacement as the dominant reaction path.
Conclusion
For nucleophilic aromatic substitution reactions, choosing the relevant frontier orbitals is critical for proper correlation of reactivity with LUMO energy. This is an important prerequisite for successful Quantum Mechanics-Machine Learning of chemical reactivity and regioselectivity [4].
Building on What We Just Learned
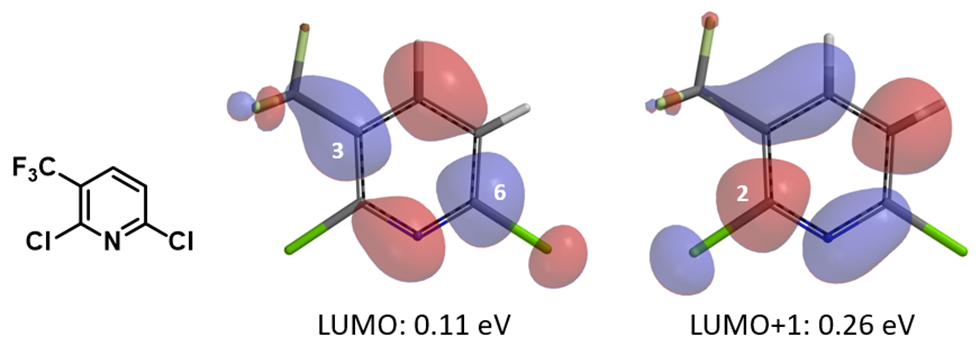
In the textbook “Heterocyclic Chemistry”[5], the authors taught us that nucleophilic substitution of 3-halopyridine is too slow for practical use. However, in the synthesis of Doravirine, a non-nucleoside reverse transcriptase inhibitor (NNRTI) for the treatment of HIV-1 infection, reaction of 3-chloro-5-iodophenol with 2-chloro-3-fluoro-4-trifluoromethyl-pyridine provides selectively the C3 substituted product [6], no displacement of the “potentially” more reactive C2 chloride is observed.
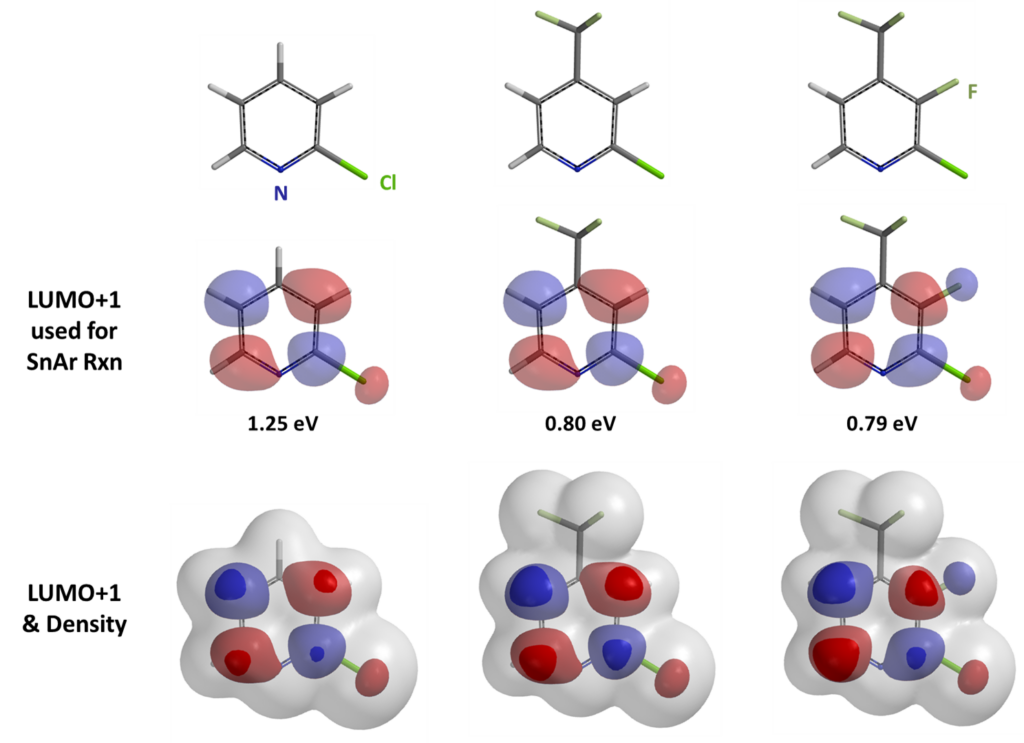
Shown below are LUMO+1 of three 2-chloropyridine analogs and their overlays with respective electron cloud density maps. Note the effects of sequential introduction of trifluoromethyl and fluoro groups on LUMO+1 energy and lobe distribution, in particular at C2 and C3 carbons. It should become obvious why SnAr of 2-chloro-3-fluoro-4-trifluoromethylpyridine proceeds selectively at C3, not at C2.
< Magical Power of Quantum Mechanics
References:
[1] J. A. Joule & K. Mills. Heterocyclic Chemistry 5th Ed. Chichester, West Sussex, UK: Blackwell Publishing Ltd., 2010; pp 25.

[2] M. Schlosser, T. Rausis, Helv. Chim. Acta. 2005, 88, 1240.
[3] G. Koleva, B. Galabov, J. I. Wu, H.F. Schaefer III, P. R. Schleyer, J. Am. Chem. Soc. 2009, 131, 14722.
[4] (a) T. Stuyver, C. W. Coley, J. Chem. Phys. 2022, 156, 084104. (b) Y. Guan, C. W. Coley, H. Wu, D. Ranasinghe, E. Heid, T. J. Struble, L. Pattanaik, W. H. Green, K. F. Jensen, Chem. Sci. 2021, 12, 2198.
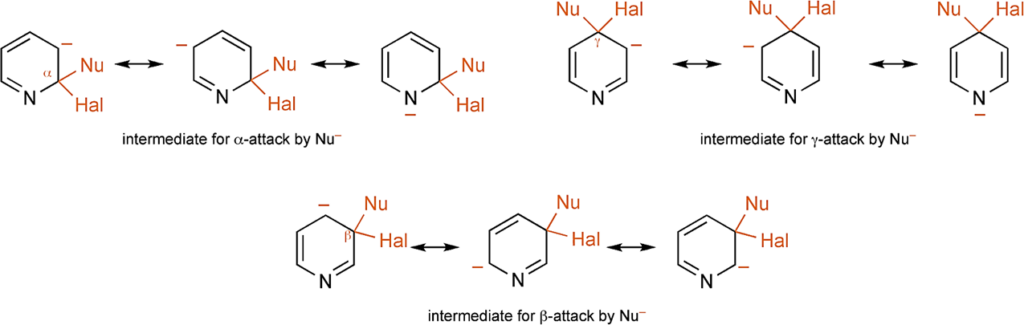
[5] J. A. Joule & K. Mills. Heterocyclic Chemistry 5th Ed. Chichester, West Sussex, UK: Blackwell Publishing Ltd., 2010; pp 118. Such substitutions follow the same mechanistic route as the displacement of halide from 2- and 4-halonitro-benzenes, i.e., the nucleophile first adds and then the halide departs. By analogy with the benzenoid situation, the addition is facilitated by: (i) the electron – deficiency at α- and γ-carbons, further increased by the halogen substituent, and (ii) the ability of the heteroatom to accommodate negative charge in the intermediate thus produced. A comparison of the three possible intermediates makes it immediately plain that this latter is not available for attack at a β-position, and thus β nucleophilic displacements are very much slower – for practical purposes they do not occur.
[6] L. C. Campeau, Q. H. Chen, D. Gauvreau, M. Girardin, K. Belyk, P. Maligres, G. Y. Zhou, C. Z. Gu, W. Zhang, L. S. Tan, P. D. O’Shea, J. Org. Process Res. Dev. 2016, 20, 1476.

