How about Tautomers?
QM Magic Class | Chapter 49
< Magical Power of Quantum Mechanics
A compound exhibits tautomerism if it can be represented by two structures that are related by an intramolecular movement of hydrogen from one atom to another. The different tautomers of a molecule usually have different molecular fingerprints, hydrophobicities, electrostatic properties, acidity, and even 3D shapes [1]. One of the most well studied tautomerizations is the interconversion of 2-hydroxypyridine and 2-pyridone. The equilibrium between these two tautomeric forms is sensitive to properties of solvent. 2-Hydroxypyridine has an OH group capable of hydrogen bonding, yet it is 2-pyridone that is better stabilized in the high polarity solvents. The equilibrium constants in different solvents are shown in Table 1 [2]. Intuitively, this is not easy to rationalize. Could QM help us to understand this dichotomy?
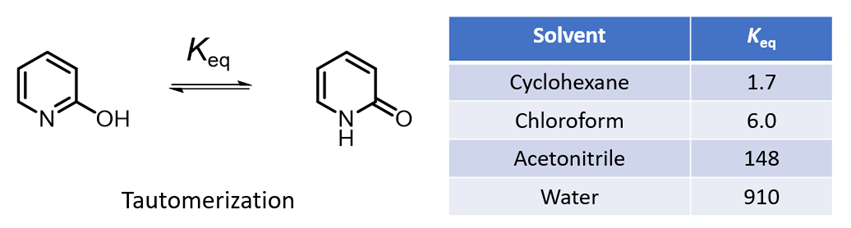
Figure 1. Solvent effect in 2-hydroxypyridine and 2-pyridone tautomers equilibria
Tautomerization between 2-hydroxypyridine and 2-pyridone
First, we calculated for the equilibrium geometry of 2-hydroxypyridine and 2-pyridone. DFT wB97X-V and a bigger basis set 6-311+G(2df,2p) are used for all the calculations discussed in this chapter [3].
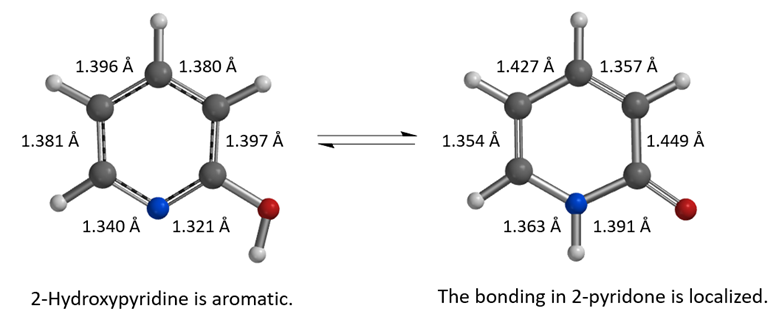
Figure 2. Equilibrium geometry of 2-hydroxypyridine and 2-pyridone, calculated with DFT wB97X-V/6-311+G(2df,2p), C-PCM model, dielectric constant 2.02, cyclohexane
As shown in Figure 2, the calculated carbon to carbon distances in 2-hydroxypyridine are 1.381 Å, 1.396 Å, 1.380 Å, 1.397 Å, suggestive of aromatic resonance. While the carbon to carbon distances in 2-pyridone alternate short and long: 1.354 Å, 1.427 Å, 1.357 Å, 1.449 Å, more consistent with localized CC single and double bonds, and the carbon to nitrogen distances in 2-pyridone are 1.363 Å and 1.391 Å, much longer than the CN distances in 2-hydroxypyridine, 1.340 Å, 1.321 Å, more consistent with CN single bonds in pyridone. These bond distance data suggest 2-pyridone is not aromatic. Experimental equilibrium constant (Keq) between 2-hydroxypyridine and 2-pyridone is 1.7 in cyclohexane (25 °C), indicative of a relatively small ~0.32 kcal/mol energy difference, with a small preference for 2-pyridone.
To understand the shift in equilibrium between these two tautomeric forms from cyclohexane to chloroform, we compared the calculated Dipole Moment of the tautomers (Figure 3).
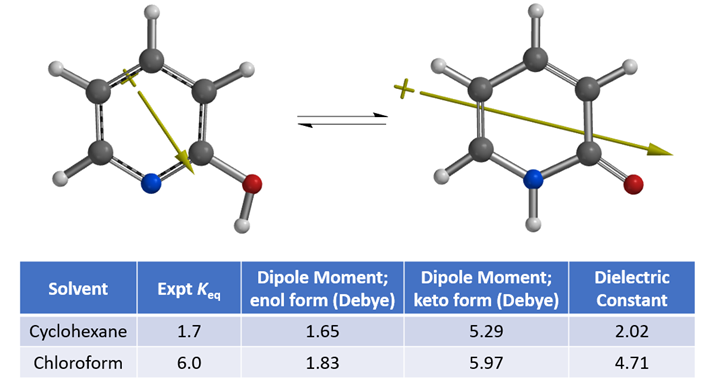
Figure 3. Equilibria between 2-hydroxypyridine and 2-pyridone and their calculated dipole moments
Calculated dipole moment[4] of 2-pyridone, 5.29 and 5.97 Debye in cyclohexane and chloroform, respectively, are higher than that of 2-hydroxypyridine, 1.65 and 1.83 Debye, respectively, as such 2-pyridone is relatively more stable than 2-hydroxypyridine in chloroform, with a higher dielectric constant than cyclohexane, accounting for the observed Keq shift from 1.7 to 6.0. The location, orientation, and size of the dipole moment vector, where the + sign refers to the positive end of the dipole, correlates with the charge distribution and degree of charge separation on the tautomers. Difference in dipole moment could also be visualized and compared with calculated Electrostatic Potential Maps as shown in Figure 4. 2-Pyridone exhibits significantly larger charge separation than 2-hydroxypyridine.
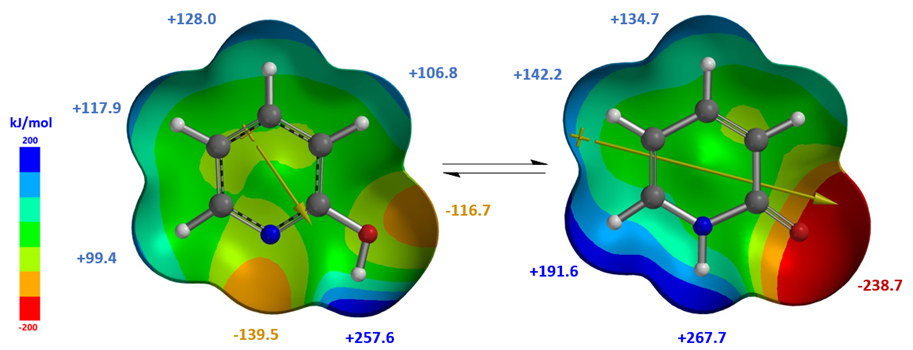
Figure 4. 2-Hydroxypyridine and 2-pyridone (Diploe/Natural Charges/Electrostatic Potential Map)
Moving from chloroform to acetonitrile and water, the changes in Keq are larger than what will be expected from differences in changes in solvents’ dielectric constant. How to account for it? We decided to focus further analyses of the 2-hydroxypyridine/2-pyridone tautomerization in the presence of water.
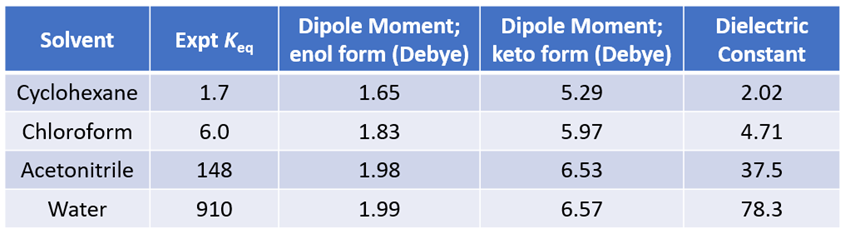
Figure 5. Equilibria between 2-hydroxypyridine and 2-pyridone and their calculated dipole moments
For the following analyses, it is important to understand:
- a. how solvation will affect the energy barrier for tautomerization between 2-hydroxy-pyridine and 2-pyridone?
- b. how water could solvate 2-pyridone, change their relative energy, shifting the tautomeric equilibrium from the hydroxy to the keto form?
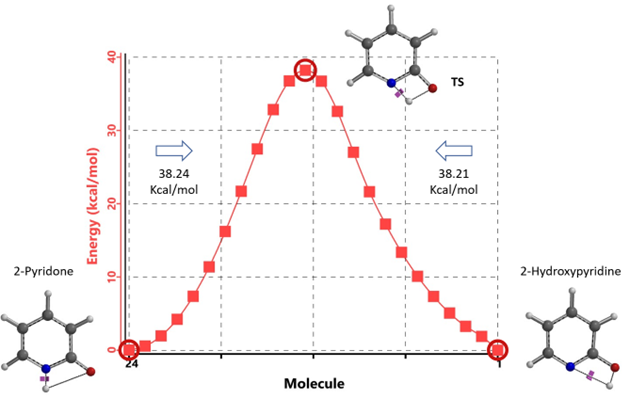
Figure 6. Intrinsic Reaction Coordinate between non-solvated 2-hydroxypyridine and 2-pyridone
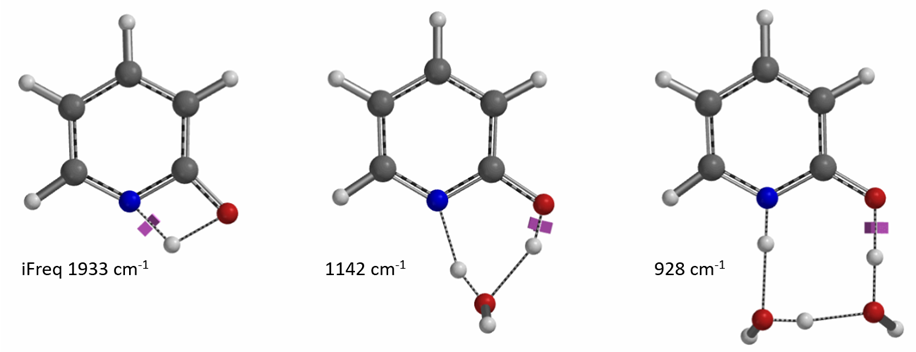
Our DFT Transition State [5] and Intrinsic Reaction Coordinate calculations show that for non-solvated equilibration between 2-hydroxypyridine and 2-pyridone, the energy barriers are 38.21/38.24 kcal/mol. Very high energy hurdles (Figure 6). This value is significantly reduced to 12.12/16.74 kcal/mol in the presence of a single water molecule bridging the N-H and C=O part of 2-pyridone (Figure 7). Further change to about 13.17/17.51 kcal/mol for the doubly solvated form (Figure 8). The presence of water molecules strongly reduces the tautomerization barrier between the tautomeric forms, and 2-pyridone water complexes are more stable than the 2-hydroxypyridine ones.
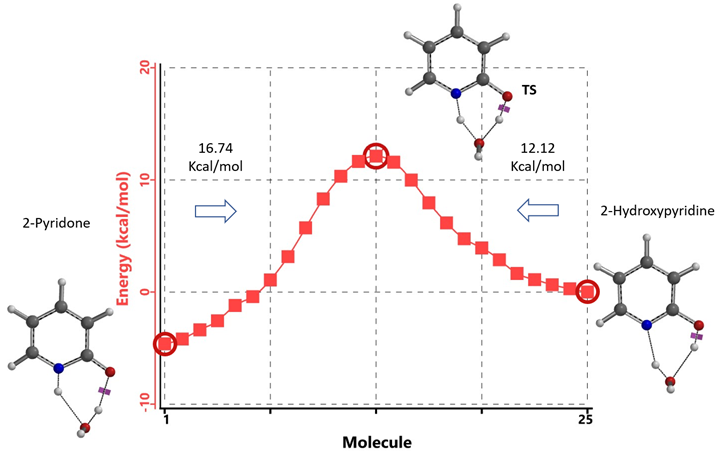
Figure 7. Intrinsic Reaction Coordinate between 2-hydroxypyridine and 2-pyridone monohydrate
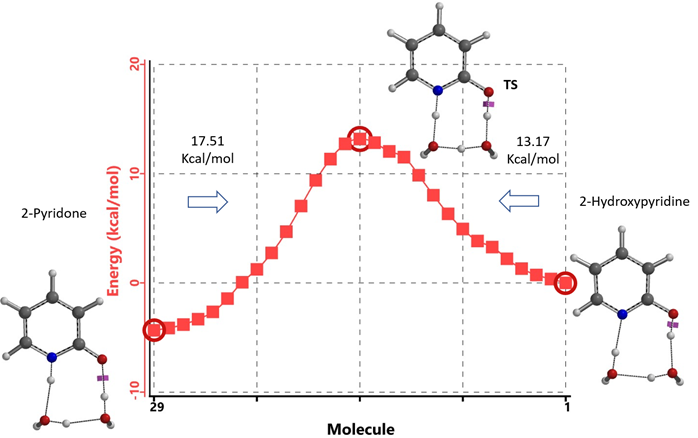
Figure 8. Intrinsic Reaction Coordinate between 2-hydroxypyridine and 2-pyridone dihydrate
Water solvates 2-pyridone via formation of hydrogen bonds and shifts the tautomeric equilibrium from the hydroxy to the keto form. Calculations with a microsolvation model show that the solvation is an energetically highly favorable process, -5.08 and -6.69 kcal/mol, respectively with incorporation of the first and second water molecule (Figure 9). The presence of these 2-hydroxypyridine and 2-pyridone hydrated complexes with one and two water molecules and the equilibrations catalyzed by water are supported experimentally with results from Molecular Beam Fourier Transform Microwave Spectroscopy [6].
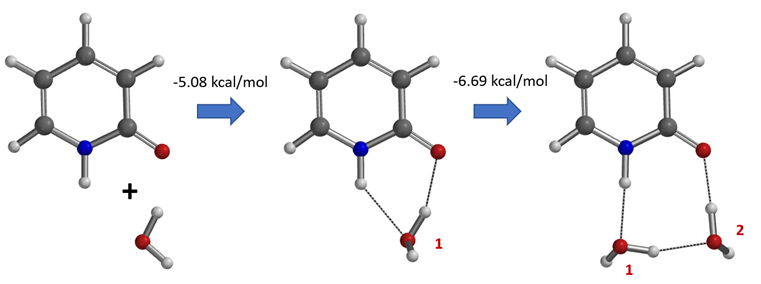
Figure 9. Microsolvation models of 2-pyridone and water
The above microsolvation models provide us semi-quantitatively a picture on how hydrogen bonding shifts Keq of 6 in CHCl3 to 910 in water, a more than 150-folds change, and the variations with Keq values reported for polar aprotic solvents, and how small amount of water complicates things. More realistic models shall have a cluster of water molecules around 2-pyridone as shown in Figure 10 for more precise evaluation of energy change in solvation.
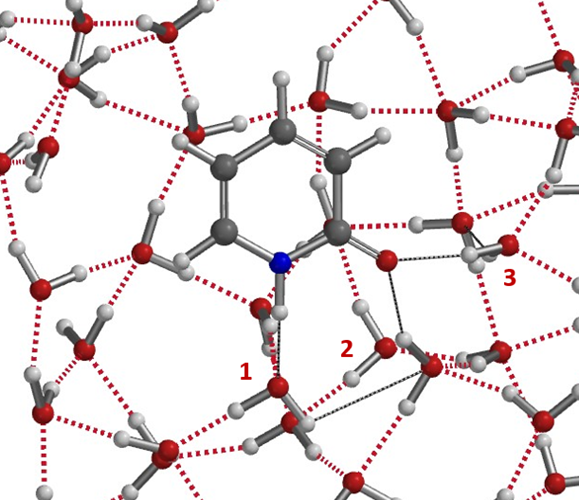
Figure 10. Water cluster model. Very likely more than two water molecules in the solvation complex.
For equilibration in the absence of water/protic solvent, our calculation revealed a concerted double proton transfer. Interestingly, the transition state (with single iFreq of 889 cm-1) calculated suggests an asynchronous process, with the N-H bond distances of 1.433 Å vs 1.206 Å and the O-H bond distances of 1.283 Å vs 1.089 Å (Figure 11) [7].
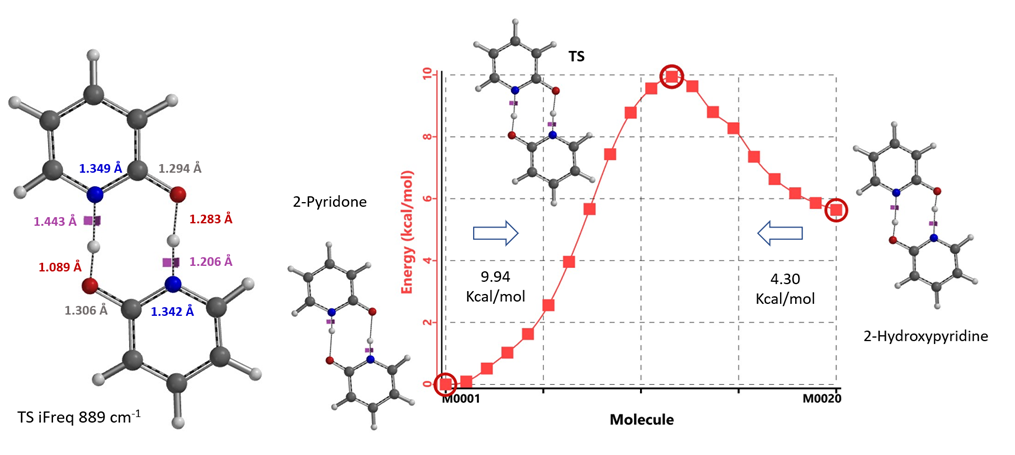
Figure 11. Transition State and IRC for equilibration in the absence of water/protic solvent
DFT analyses help us to understand why Keq of 2-hydroxypyridine and 2-pyridone is highly solvent dependent, and why a little water complicates analyses in polar aprotic solvents.
Tautomerism of 10-hydroxy-1,7-phenanthrolines
10-Hydroxy-1,7-phenanthrolines, structurally related to 4-pyridone, exhibit unique tautomerism features (Figure 12). The system was studied by Katritzky et al. extensively in the nineties [8, 9, 10], found to be less sensitive to change in polarity of solvents, and merits revisit with further QM analyses. “Generate Tautomers” tool [11] added tautomer C to the list of two, A & B, reported earlier for consideration.
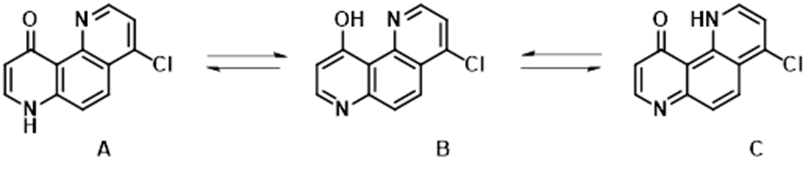
Figure 12. 4-Chloro-10-hydroxy-1,7-phenanthroline tautomers
Our DFT calculated electron density contour maps of 4-chloro-10-hydroxy-1,7-phenanthroline show strong intramolecular hydrogen bonding in enol form B and keto form C. There is significantly less electron density between the C=O oxygen and pyridine N in keto form A. Infrared red spectra in nujol, CCl4, or CHCl3 exhibit broad absorption ca. 2300–3500 cm-1, indicative of strong hydrogen bonding, suggesting that tautomer A is a minor species [8].
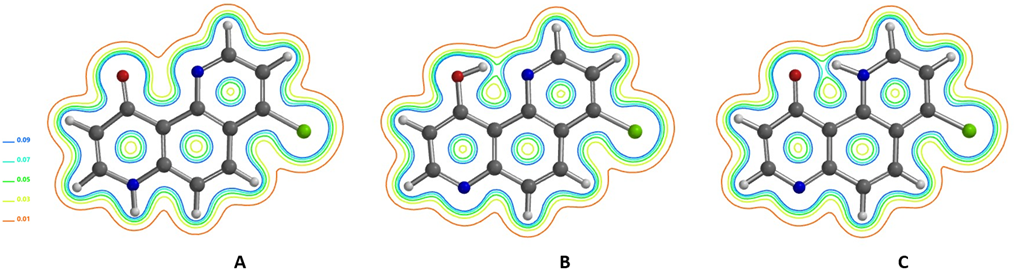
Figure 13. Electron density contour maps of 4-chloro-10-hydroxy-1,7-phenanthroline tautomers A, B, C
DP4[12] analysis of QM calculated 13C NMR of 4-chloro-10-hydroxy-1,7-phenanthroline A, B, C tautomers versus experimental data[10] (Figure 14) provides DP4 scores of 0%, 100%, 0%, respectively; and DFT calculated equilibrium geometry relative energy of 6.33, 0.00, 5.83 kcal/mol, respectively, provide strong support that the intramolecularly hydrogen bonded enol B is the predominate tautomer. Among the two keto forms, tautomer C, with an intramolecular hydrogen bond, is lower in energy than tautomer A.
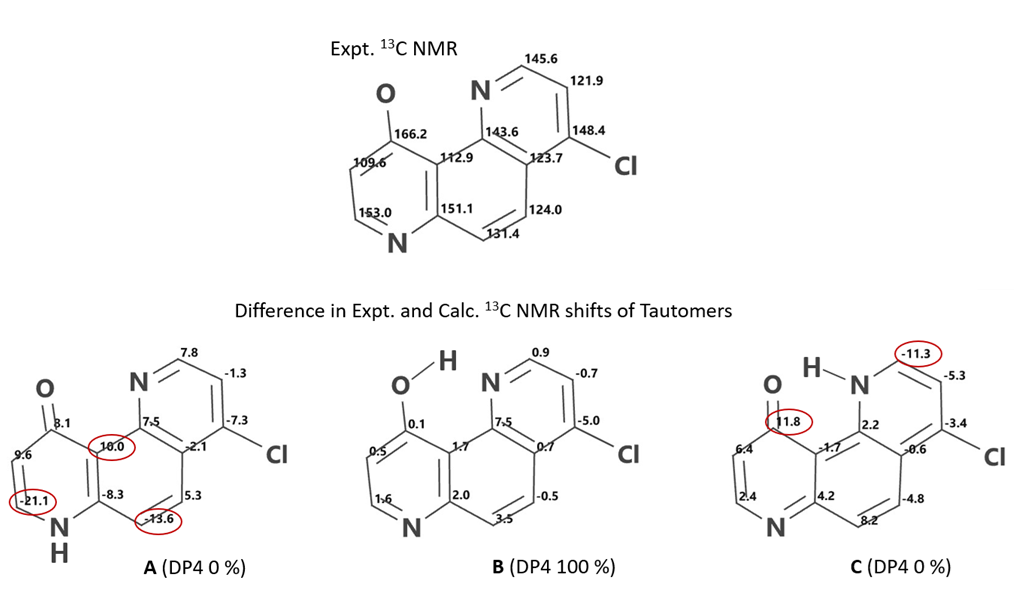
Figure 14. Expt 13C NMR of 4-chloro-10-hydroxy-1,7-phenanthroline | Difference in Expt. and Calc. 13C NMR shifts of tautomers A, B, C, and their DP4 scores
Energy barriers calculated for equilibration are ~ 0.50 kcal/mol from keto C to enol B and 6.31 kcal/mol in reverse, suggesting that equilibration will proceed rapidly at room temperature.
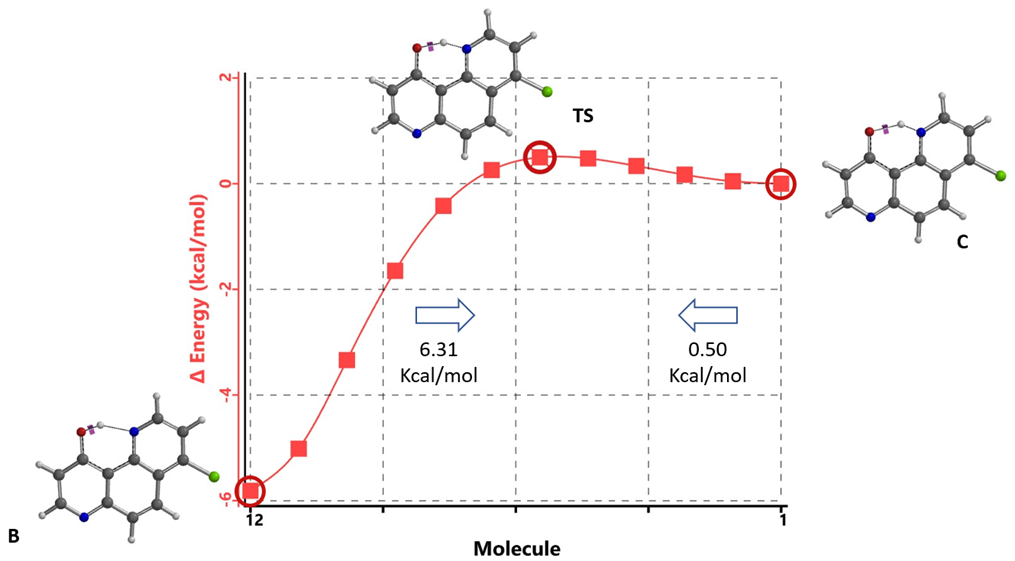
Figure 15. Intrinsic Reaction Coordinate between tautomer B and C
It is note-worthy to point out that, unlike the tautomerism between 2-hydroxypyridine and 2-pyridone, for tautomers with strong intramolecular hydrogen bond, in general, the Keq are less sensitive to change in polarity of solvents [10].
Retrospect
Tautomer identification is especially important in dealing with heterocyclic compounds where two or more different tautomers may exist in equilibrium, and the identity of the dominant species may not be intuitively obvious. Precise experimental determination and QM analyses of tautomerization equilibria are significant challenges. Complexity and uncertainty multiply with tautomeric structures in MedChem design. Local charged or polar groups in the binding pockets can shift the tautomer ratios and binding to the higher energy tautomer in free solution. All these make tautomerization easy to ignore but overwhelming to consider[1]. QM may not be able to precisely quantify the small energy difference between tautomers in solution, yet it is highly reliable in differentiating tautomers with ≥10 kcal/mol difference. It is unlikely that 10 kcal/mol could be compensated by protein binding to arrive at low nano molar potency candidates suitable for clinical development, while a tautomeric energy difference of a few kcal/mol could be more readily compensated. Binding with tautomeric forms which are significantly different in energy could benefit from Fragment Molecular Orbital analyses [13, 14, 15]. QM tools for tautomerization analyses are readily accessible and shall be used routinely for target design and prioritization.
Building on What We Just Learned
ү-Hydroxybutenolideg-Hydroxybutenolide is an important structural core found in many bioactive marine natural products such as Palauolide [16], Cacospongionolide A, Dysidiolide, Manoalide [17], etc., and considered to be the key pharmacophore for this class of compounds with diverse biological properties.
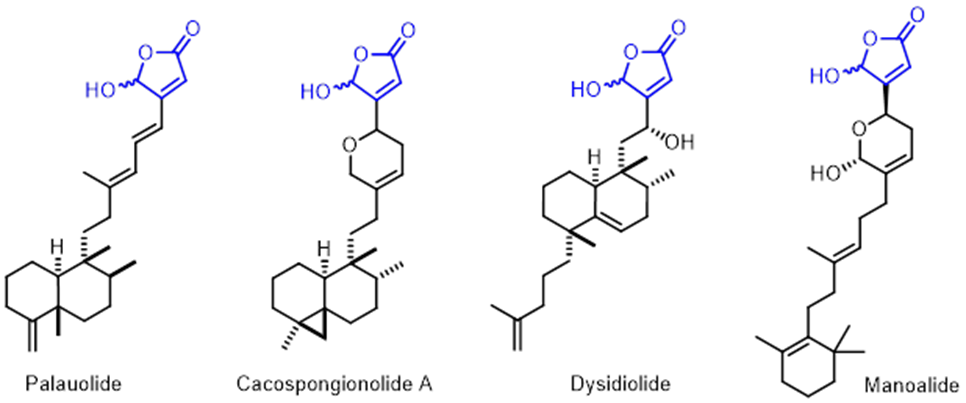
Figure 16. Selected natural products with ү-hydroxybutenolide moiety
Looking at the structures of these important natural products, obvious questions arise.
- a. Why the hydroxyl group is always on the more substituted side of the butenolide?
- b. Based on the relative energy of three tautomeric forms shown below, will g-hydroxy-butenolide equilibrate to other tautomeric forms?

Figure 17. Potential g-hydroxybutenolide tautomerization mechanism
References:
[1] Y. C. Martin J. Comput. Aided Mol. Des., 2009, 23, 693.
[2] E.V. Anslyn, D.A. Dougherty (2006) Modern Physical Organic Chemistry. New York, NY, USA: University Science Books; page 155.
[3] For DFT calculation of tautomers, wB97X-V/6-311+G(2df,2p) is a more accurate model than the standard wB97X-D/6-31G* one we routinely used for other QM calculations.
[4] Spartan’20 Tutorial and User’s Guide (2020). Irvine, CA, USA: Wavefunction, Inc. page 50.
[5] Transition States calculated for tautomeric equilibration between 2-hydroxypyridine and 2-pyridone in the presence of zero, one, and two water molecules.
[6] S. Mata, V. Cortijo, W. Caminati, J. L. Alonso, M. Eugenia Sanz, J. C. López, S. Blanco J. Phys. Chem. A 2010, 114, 11393.
[7] A. Fu, H. L. Li, D. M. Du, Z. Y. Zhou J. Phys. Chem. A 2005, 109, 1468. This paper studied the 2-pyridone dimer tautomer equilibration with B3LYP and BH-LYP hybrid density functional methods at the 6-311++G (2d, 2p) basis set level. Results suggest the process to be concerted and synchronous. E. Torres, G. A. DiLabio, J. Phys. Chem. Lett. 2012, 3, 1738 noted that B3LYP is not able to reliably model systems in which noncovalent interactions are important (hydrogen bonding, π-stacking, etc.).
[8] I. Shcherbakova, J. Elguero, A. R. Katritzky Advances in Heterocyclic Chemistry, 2000, 51.
[9] A. R. Katritzky, M. Karelson, P. A. Harris Heterocycles 1991, 32, 329.
[10] A.R. Katritzky, I. Ghiviriga, P. Leeming, F. Soti Magnetic Resonance in Chemistry, 1996, 34, 518.
[11] Tautomer Generators
a. Spartan’20 Tutorial and User’s Guide (2020). Irvine, CA, USA: Wavefunction, Inc. page 269. Spartan’20 tautomer generating tool is limited to tautomers involving nitrogen, oxygen, phosphorus, and sulfur. Tautomers involving carbon have intentionally been excluded. And as such Spartan’20 “Generate Tautomer” does not alert the possibility of the keto form as shown below.

Figure 18. Spartan’20 Tautomer Generation Tool
b. D. K. Dhaked, W.-D. Ihlenfeldt, H. Patel, V. Delannée, M. C. Nicklaus J. Chem. Inf. Model. 2020, 60, 1253. Tautomerizer is a more thorough tautomer generator. This web tool is available at https://cactus.nci.nih.gov/tautomerizer/
[12] S. G. Smith, J. M. Goodman J. Am. Chem. Soc, 2020, 132, 12946. T.-H. Duong, M. A. Beniddir, J. Boustie, K.-P.-P. Nguyen, W. Chavasiri, G. Bernadat, P. Le Pogam Molecules, 2019, 24, 1527.
[13] M. Wieder, J. Fass, J. D. Chodera Chem. Sci. 2021, 12, 11364.
[14] H. Brandstetter. F. Grams, D. Glitz, A. Lang, R. Huber. W. Bode, H-W. Krell, R. A. Engh J. Biol. Chem. 2001, 276, 17405. Based on a 1.8-Å crystal structure of human neutrophil collagenase (MMP-8) in complex with an active site-directed inhibitor (RO200-1770; https://www.rcsb.org/structure/1jj9), authors concluded that the inhibitor binds in the enol form, which is 17.14 kcal/mol higher in energy than the keto form.
[15] For recent reviews on Fragment Molecular Orbital Analyses, see Alexander Heifetz editor Quantum Mechanics in Drug Discovery, 2020, Springer Science+Business Media, LLC, New York, NY 10004, U.S.A. Guiding Medicinal Chemistry with Fragment Molecular Orbital (FMO) Method. pp. 37-48, Analyzing Interactions with the Fragment Molecular Orbital Method pp. 49-73.
[16] T. Mai, J. Toullec, S. Van Wynsberge, M. Besson, S. Soulet, S. Petek, E. Aliotti, M. Ekins, K. Hall, D. Erpenbeck, D. Lecchini, M. A. Beniddir, D. Saulnier, C. Debitus Fish. Aquatic Sci. 2019, 22, 30.
[17] S. Tilvi, S. Khan, M.S. Majik Current Org. Chem. 2019, 23, 2436.

